XGBoost

### XGBoost树的定义
先来举个例子：
我们要预测一家人对电子游戏的爱好程度，考虑到年龄因素，年轻人比老年人更喜欢电子游戏，考虑到日常是否使用电脑，年轻人日常使用电脑更多一些，于是我们可以构造出如下两棵决策树：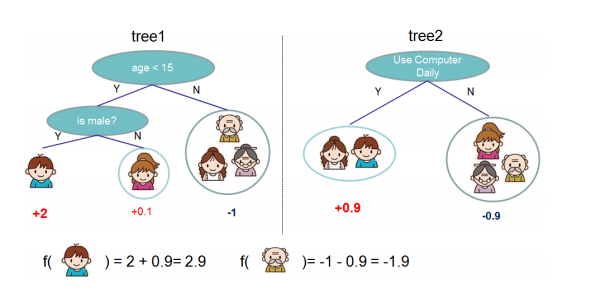

![](/media/202212/quesbase64153438578739198433_1671783555.png)

将两棵树的结论累加起来得到最终的结论：
- 小孩的总分是：2+0.9=2.9
- 爷爷的总分是：-1-0.9=-1.9

因此我们认为小孩更喜欢电子游戏。

那么问题来了，这与`GBDT`有什么不同吗？好像**都是构造多棵决策树进行累加**。
实际上，`XGBoost`与`GBDT`最大的不同在于损失函数，或者称为目标函数。
- `GBDT` 规定了使用xxx作为损失函数；
- `XGBoost` 没有规定使用哪种损失函数，你可以自己选择，比如使用**均方误差损失函数**，或者使用**交叉熵损失函数**(也称为**对数损失函数**)；

### XGBoost 原理一：获取损失函数
> 我们首先约定：
$$n$$: 表示特征数量；
$$m$$: 表示样本数量；
$$a$$: 表示叶子结点数量；
$$i$$: 表示第$$i$$个特征；
$$j$$: 表示第$$j$$个样本；
$$k$$: 表示第$$k$$个叶子结点；

对于一个有$$n$$个特征$$m$$个样本的样本集，`xgboost`会有如下过程：
对每个特征$$x_i$$构造一棵决策树$$T_i$$，树的叶子结点就是分类结果，假设$$T_i$$有$$a$$个叶子结点，也就是说特征$$x_i$$有$$a$$种分类结果，每个分类结果的值记为$$r_k$$（其中$$k=1,2,...,a$$），那么，这棵树的损失函数记为：
> **树的损失函数**
> ```latex
> L_i = min\sum_{t=1}^{m} L(y_t, \hat{y_t})
> ```

对于$$T_i$$的一个叶子结点$$node_k$$，它的值为$$r_k$$(意味着它的预测值为$$r_k$$)，它的样本集$$I_k$$包含了一个或多个样本，那么该叶子结点的损失函数为：
> **叶子结点的损失函数 v1.0**
> ```latex
> L_{ik} = \sum_{t\in I_k}L(y_t, r_k+\hat{y_t}^{(i-1)})
> ```

> 其中，$$r_k$$是我们要计算的变量，我们要算出$$r_k$$为多少时可以使得$$L_{ik}$$最小；
> 需要注意的是，这里的$$\hat{y_t}^{(i-1)}$$，其实是前面$$i-1$$棵树预测值的累加值，因为每一棵树拟合的都是残差；

所以整棵树的损失函数可以根据叶子结点改写为：
```latex
L_i = min\sum_{k=1}^{a}L_{ik}
```
由于不同的叶子结点相互独立，互不干扰，它们的损失值仅仅取决于自己的预测值，因此整棵树的损失函数可以写为：
> **树的损失函数**
> ```latex
> L_i = \sum_{k=1}^{a}minL_{ik}
> ```

因此，我们只要计算出每个叶子结点的最小损失，并将它们相加，就可以得到整棵树的最小损失。

### XGBoost 原理二：使用泰勒展开式处理损失函数
> **泰勒展开式**
> ```latex
> f(x)\approx f(x_0) + f'(x_0)(x-x_0)+\frac{1}{2}f''(x_0)(x-x_0)^2
> ```

`xgboost`主要是对损失函数使用了泰勒展开式，我们来逐步分析。
我们通过前面的分析得到了这样一个公式：
> 第$$i$$棵树，第$$k$$个叶子结点，包含的样本集合为$$I_k$$，该叶子结点的损失值为：
> ```latex
> L_{ik} = \sum_{t\in I_k}L(y_t, r_k+\hat{y_t}^{(i-1)})
> ```

由于$$y_t$$和$$\hat{y_t}^{(i-1)}$$都是常量，只有$$r_k$$是变量，所以上面公式可以写成这样：
```latex
L_{ik} = \sum_{t\in I_k}L(r_k+\hat{y_t}^{(i-1)})
```
然后令`$$x=r_k+\hat{y_t}^{(i-1)}$$`,`$$x_0=\hat{y_t}^{(i-1)}$$`，则`$$x-x_0=r_k$$`
根据泰勒展开式可以得到：
> **叶子结点的损失函数 v2.0**
>```latex
> L_{ik} = \sum_{t\in I_k}L(r_k+\hat{y_t}^{(i-1)}) \qquad \qquad \qquad \qquad \qquad \quad \quad \quad \ \\
> \ \\
> \approx \sum_{t\in I_k}(L(\hat{y_t}^{(i-1)})+L'(\hat{y_t}^{(i-1)})r_k+\frac{1}{2}L''(\hat{y_t}^{(i-1)})r_k^2)
> ```

在损失函数选定的情况下，可以获得该损失函数的一阶导数和二阶导数，然后将上一颗树的计算结果带入导函数中，就可以获得当前这棵树所需要的计算参数。因此在计算过程中，每计算一棵树就要更新梯度值（一般用g表示一阶梯度，h表示二阶梯度）。

> **举个例子**
> 我们选择平方误差损失函数，则对于第$$j$$个样本，有如下公式：
> ```latex
> L = (y_j-\hat{y_j})^2 \\
> L'= 2(y_j-\hat{y_j}) \\
> L''=2 \qquad\quad \ \ 
> ```
> 由于$$y_i$$是已知的数值，我们只需要将前一棵树的预测值带入进去，就可以获得当前这棵树所需要的计算参数

### 寻找最佳分割点
结点在分裂时，需要选择一个特征和特征值作为分割点，寻找最佳分割点的步骤如下：
1. 遍历每个结点的每个特征；
2. 对每个特征，按特征值的大小进行排序；
3. 扫描每个特征的所有特征值，找出每个特征的最佳分裂特征值；
4. 在所有特征中找出最好的分裂点（增益最大的特征和特征值）；

上面的方法会扫描所有的特征和特征值，在数据量较大的时候会很慢，因此，XGBoost提出了一系列加快寻找最佳分裂点的方案：
1. `特征预排序并缓存`：XGBoost在开始训练前，预先对每个特征的值进行排序，后面的计算会重复使用这个缓存，减少排序的工作量；
2. `分位点近似法`：对每个特征排序后，采用类似分位点选取的方式，仅仅选出常数个特征值作为该特征的候选分割点，在寻找特征的最佳分割点时，从候选分割点中选择最优的一个；
3. `并行查找`：在结点分裂时，可以并行计算不同特征的最佳分割点，极大的提升了运行速度；

### 叶子结点权重
```latex
w_j=-\frac{G_j}{H_j+\lambda}
```

### 目标函数Obj
> `目标函数` = `损失函数` + `正则化项`
```latex
obj=-\frac{1}{2}\sum_{j=1}^T\frac{G_j^2}{H_j+\lambda}+\gamma T
```

### 结点分裂的增益Gain
> `分裂的增益：` 等于 父节点的损失减去两个孩子结点的损失，如果差值大于0，说明有增益，可以分裂；如果小于0，说明没有增益，不能分裂。
```latex
Gain=\frac{1}{2}(\frac{G_L^2}{H_L+\lambda}+\frac{G_R^2}{H_R+\lambda} - \frac{(G_L+G_R)^2}{H_L+H_R+\lambda})-\gamma
```

### 一阶梯度g和二阶梯度h
损失函数使用`对数损失(logloss)`：
```latex
L(y_i, \hat{y_i})=y_iln(1+e^{\hat{y_i}})+(1-y_i)ln(1+e^{\hat{y_i}})
```
其中，$$i$$表示第$$i$$个样本， $$\hat{y_i}$$为该样本所在的叶子结点的权重之和。
令：
```latex
p_i=\frac{1}{1+e^{\hat{y_i}}}
```
可以求得损失函数的一阶梯度为：
```latex
g_i=p_i-y_i
```
二阶梯度为：
```latex
h_i=p_i(1-p_i)
```

### 参考
> [XGBoost算法](https://www.cnblogs.com/mantch/p/11164221.html)
> [XGBoost拟合的是什么](https://www.zhihu.com/question/269929168)
> [XGBoost、GBDT超详细推导](https://zhuanlan.zhihu.com/p/92837676)