前馈神经网络

### 基本概念
前馈神经网络由多层神经元组成，层间的神经元互相连接，层内的神经元不连接。其信息处理机制是：前一层神经元通过层间连接向后一层神经元传递信号。因为信号是从前往后传递的，所以是“前馈的”信息处理网络。
神经元是对多个输入信号(实数向量)进行非线性转换产生一个输出信号(实数值)的函数。整个神经网络是对多个输入信号(实数向量)进行多次非线性转换产生多个输出信号(实数向量)的复合函数。

#### 神经元
神经元是如下定义的非线性函数：
```latex
y = f(x)=a(\sum_{i=1}^{n}w_{i}x_{i}+b )
```
或者写作：
```latex
y=f(x)=a(z)\quad \\
\ \\
z=\sum_{i=1}^{n}w_{i}x_{i}+b 
```

>$$x_{1},x_{1},···,x_{n}$$是输入，取实数值；
$$y$$是输出，取实数值；
$$z$$是中间结果，又称为**净输入**，也是实数值；
$$z=wx+b$$是仿射函数；
$$a$$是特定的非线性函数，称为激活函数

神经元函数由两部分组成：
1. 使用`仿射函数`对输入向量进行`线性变换`，得到净输入z；
2. 使用`激活函数`对净输入z进行`非线性变换`，得到输出y；

#### 中间层神经元的激活函数
1. `S型函数`
```latex
f(x)=\frac{1}{1+e^{-x}}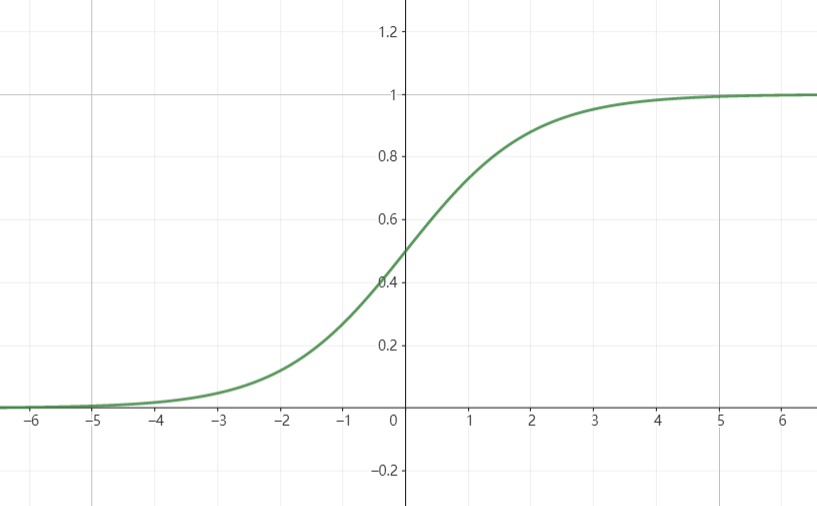
```
![](/media/202211/微信截图_20221113102931_1668306586.png)

2. `双曲正切函数tanh`
```latex
f(x)=\frac{e^{x} - e^{-x}}{e^{x} + e^{-x}}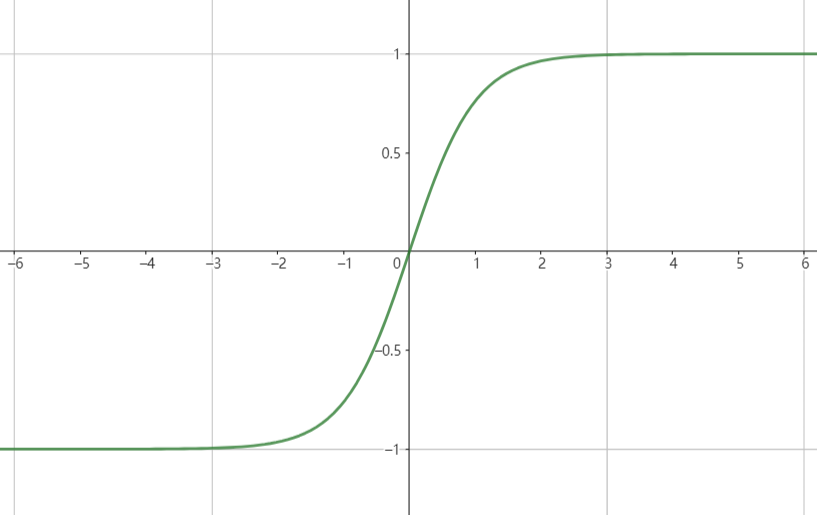
```
![](/media/202211/222_1668306957.png)
3. `整流线性函数relu`
```latex
f(x)=max(0, x)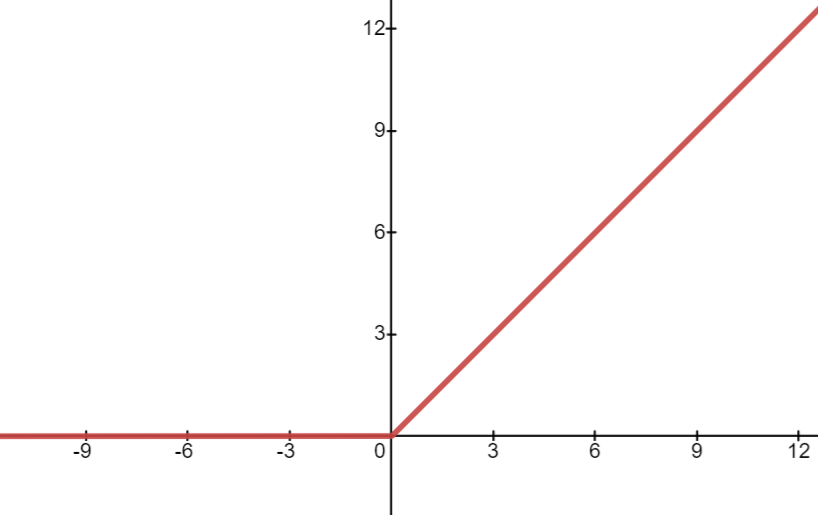
```
![](/media/202211/333_1668307820.png)

#### 输出层神经元的激活函数
输出层神经元的激活函数通常使用恒等函数/S型函数/软最大化函数，在不同的场景使用不同的激活函数。
1. 在回归场景，输出层只有一个神经元，其激活函数是恒等函数；
神经元函数如下：
```latex
z = wh_{s-1}+b \\
y=g(z)=z \ \ 
```
>其中：
$$w$$是权重向量；
$$b$$是偏置；
$$g$$是恒等函数；
$$h_{s-1}$$是第s-1层的输出；

这样的输出层也称为线性输出层。

2. 在二分类场景，输出层只有一个神经元，其激活函数是S型函数；
神经元函数如下：
```latex
z = wh_{s-1}+b \quad\quad\quad\quad\ \ \\
P(y=1) = g(z) = \frac{1}{1+e^{-z}} \\
```
3. 在多分类场景，输出层只有一个神经元，其激活函数是软最大化函数；
4. 在多标签分类场景，输出层有m个神经元，每个神经元的激活函数都是S型函数；
神经元函数如下：
```latex
z_{k} = w_{k}h_{s-1}+b_{k}\quad \quad \quad \quad \ \ \\
P(y_{k}=1)=g(z_{k})=\frac{1}{1+e^{-z_{k}}}
```
其中，$$k=1,2,···,m$$
### 模型使用场景
前馈神经网络可以作为机器学习模型用于不同的任务，有以下几种使用场景：
- 回归场景
- 二分类场景
- 多分类场景
- 多标签分类场景

### 参考
> 函数图像绘制1：[geogebra](https://www.geogebra.org/graphing?lang=zh_CN)
> 函数图像绘制2：[desmos](https://www.desmos.com/calculator?lang=zh-CN)